Discrete-Event Control
Cyber-physical control system are often implemented using digital computers that sample sensors and command inputs to actuators. This discrete implementation contrasts with the underlying continuous physics of a system. My work has focused on rigorously constructing stabilizing and safety-critical controllers in this setting, either through efficient event-triggered formulations, or using approximate discrete time models and convex optimization.
Safety of Sampled-Data Systems with Control Barrier Functions via Approximate Discrete Time Models
Andrew J. Taylor, Victor D. Dorobantu, Ryan K. Cosner, Yisong Yue, and Aaron D. Ames, in Proceedings of the IEEE 61st Conference on Decision and Control (CDC), Cancún, Mexico, 2022.
Abstract: Control Barrier Functions (CBFs) have been demonstrated to be powerful tools for safety-critical controller design for nonlinear systems. Existing CBF-based design paradigms do not address the gap between theory (controller design with continuous time models) and practice (the discrete time sampled implementation of the resulting controllers); this can lead to poor closed-loop behavior and violations of safety for hardware instantiations. We propose an approach to close this gap by synthesizing sampled-data counterparts to these CBF-based controllers using approximate discrete time models and Sampled-Data Control Barrier Functions (SD-CBFs). Using properties of a system’s continuous time model, we establish a relationship between SD-CBFs and a notion of practical safety for sampled-data systems. Furthermore, we construct convex optimization-based controllers that formally endow nonlinear systems with safety guarantees in practice. We demonstrate the efficacy of these controllers in simulation.
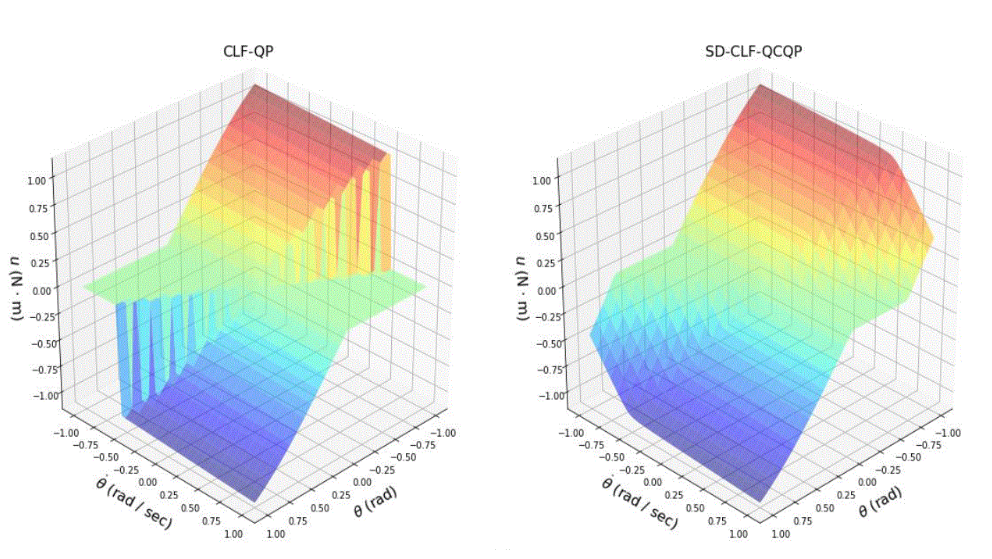
Sampled-Data Stabilization with Control Lyapunov Functions via Quadratically Constrained Quadratic Programs
Andrew J. Taylor, Victor D. Dorobantu, Yisong Yue, Paulo Tabuada, and Aaron D. Ames, IEEE Control Systems Letters, vol. 6, pp. 680-685, 2021.
Abstract: Controller design for nonlinear systems with Control Lyapunov Function (CLF) based quadratic programs has recently been successfully applied to a diverse set of difficult control tasks. These existing formulations do not address the gap between design with continuous time models and the discrete time sampled implementation of the resulting controllers, often leading to poor performance on hardware platforms. We propose an approach to close this gap by synthesizing sampled-data counterparts to these CLF-based controllers, specified as quadratically constrained quadratic programs (QCQPs). Assuming feedback linearizability and stable zero-dynamics of a system’s continuous time model, we derive practical stability guarantees for the resulting sampled-data system. We demonstrate improved performance of the proposed approach over continuous time counterparts in simulation.
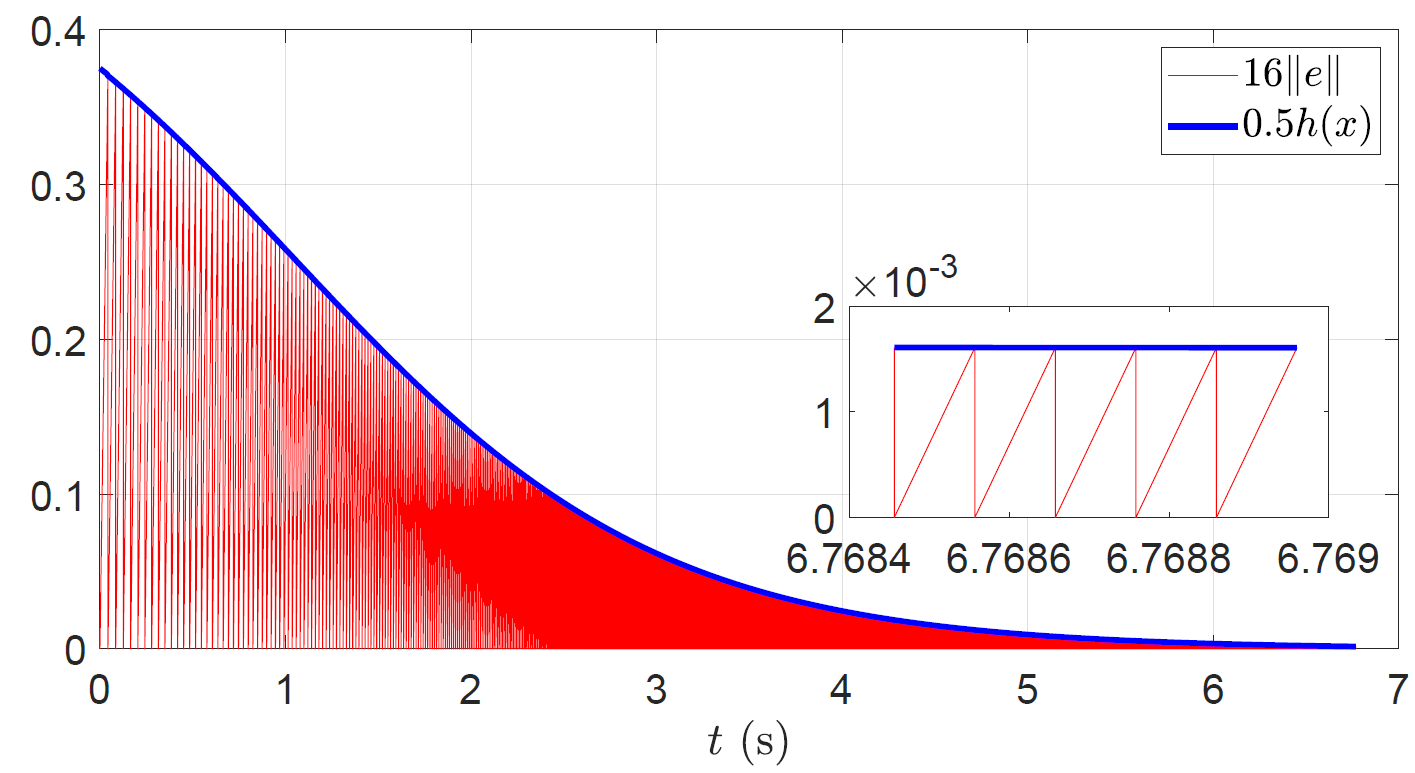
Safety-Critical Event-Triggered Control via Input-to-State Safe Barrier Functions
Andrew J. Taylor, Pio Ong, Jorge Cortés, and Aaron D. Ames, IEEE Control Systems Letters, vol. 5, no. 3, pp. 749-754, 2021.
Abstract: The efficient utilization of available resources while simultaneously achieving control objectives is a primary motivation in the event-triggered control paradigm. In many modern control applications, one such objective is enforcing the safety of a system. The goal of this paper is to carry out this vision by combining event-triggered and safety-critical control design. We discuss how a direct transcription, in the context of safety, of event-triggered methods for stabilization may result in designs that are not implementable on real hardware due to the lack of a minimum interevent time. We provide an example showing this phenomena and, building on the insight gained, propose an event-triggered control approach via Input-to-State Safe Barrier Functions that achieves safety while ensuring that interevent times are uniformly lower bounded.