Adaptive Control for Safety-Critical Systems
Adaptive control is a classic tool for resolving parametric errors in a system model by estimating parameters online as a system evolves. My work has focused on extending these classical tools to the task of safety-critical control while understanding fundamental limits on safety in the face of parametric model error.
Adaptive Safety Using Control Barrier Functions and Hybrid Adaptation
Mohamed Maghenem, Andrew J. Taylor, Aaron D. Ames, and Ricardo G. Sanfelice, in Proceedings of the IEEE American Control Conference (ACC), New Orleans, LA, USA, 2021, pp. 2418-2423.
Abstract: This paper presents a hybrid adaptive law for safety-critical adaptive control of constrained continuous-time systems under the effect of unknown disturbances. The proposed adaptive law features a hybrid update law that, using a hysteresis-type mechanism, appropriately resets the estimate of the disturbance. In contrast to continuous-time adaptation laws for safety-critical control, our hybrid adaptive law relaxes the assumption typically imposed on the unknown disturbances as well as the behavior usually imposed around the boundary of the safe region. We illustrate the benefits of the proposed hybrid law in an adaptive cruise control problem.
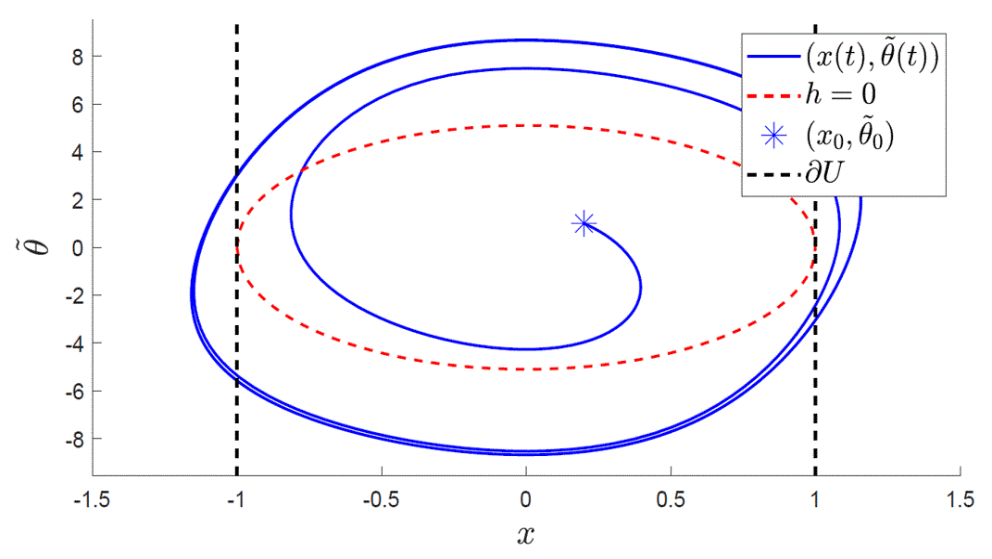
Adaptive Safety with Control Barrier Functions
Andrew J. Taylor and Aaron D. Ames, in Proceedings of the IEEE American Control Conference (ACC), Denver, CO, USA, 2020, pp. 1399-1405.
Abstract: Adaptive Control Lyapunov Functions (aCLFs) were introduced 20 years ago, and provided a Lyapunov-based methodology for stabilizing systems with parameter uncertainty. The goal of this paper is to revisit this classic formulation in the context of safety-critical control. This will motivate a variant of aCLFs in the context of safety: adaptive Control Barrier Functions (aCBFs). Our proposed approach adaptively achieves safety by keeping the system’s state within a safe set even in the presence of parametric model uncertainty. We unify aCLFs and aCBFs into a single control methodology for systems with uncertain parameters in the context of a Quadratic Program (QP) based framework. We validate the ability of this unified framework to achieve stability and safety in an Adaptive Cruise Control (ACC) simulation.